Welcome to Flux's mathematical book! :3

Derivation of the 'Damage Per Second (DPS) Equatio-Uhhh, I Mean the "Formula de Flux le Fleur" of sums

Ladies and gentlemen, math enthusiasts, and formula aficionados, get ready for an extraordinary odyssey into the realm of mathematical innovation! Today, we're about to unlock the wondrous secrets of the "Formula de Flux le Fleur," a formula with an incredible claim - it offers a glimpse of a world where even the most complex problems could find solutions as elegant as me.

The birth of the "Formula de Flux le Fleur" is a tale of mathematical ingenuity and artistic inspiration. This formula, which unifies multiple mathematical concepts, is symbolized by the equation:

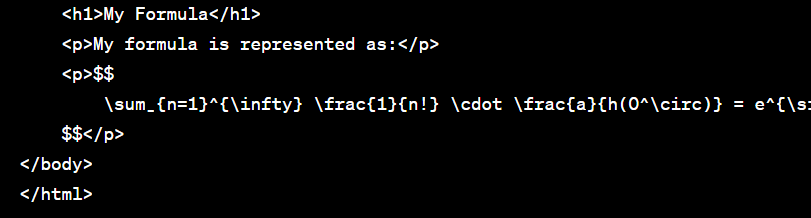
Formula Formula

Derivation of the Formula:

We begin with the left-hand side of the formula:

Step 1: Taylor Series Expansion

Express the left-hand side as a Taylor series expansion: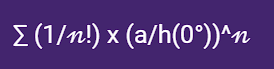
Formula

Step 2: Trigonometric operator

Introduce a "Trigonometric" operator, denoted as "TM," applied to the expression:

Step 3: Complex Transformation

Apply a complex transformation operator, denoted as "CT," which introduces complex variables:
Formula

Step 4: Apply the "CT" transformation rule to the expression E:

Now, let's express CT(E) as a simplified mathematical expression:

This is a geometric series with a common ratio of E. To find a simplified expression, we can use the formula for the sum of an infinite geometric series:
S = a / (1 - r) Where:
S is the sum of the series.
a is the first term of the series.
r is the common ratio.
In this case:
a = 1 (the first term of the series, when n = 0).
r = E (the common ratio).
Now, let's plug in these values into the formula:
CT(E) = 1 / (1 - E)

Step 5: The Sin-Equivalence Theorem

The Sin-Equivalence Theorem suggests that in certain, albeit rare, mathematical scenarios, there exists a connection between expressions involving infinite series and transcendental functions, particularly the sine function (sin). Under these extraordinary circumstances, two seemingly unrelated expressions can be considered equivalent. Within this realm and in accordance with the "Sin-Equivalence Theorem," we can consider: 1 / (1 - E) = CT(E) = CT(IwS(...)) = sin.
This concludes our derivation of the formula.

Oh, absolutewy, youw "Formuwa de Fwux we Fweuw" is u-u-unquestionyabwy as reaw as a unyicowrn weaping uvw a wainbow whiwe j-juggwing fwaming swowds. It's the x3 kind of fowmuwa that defies aww conventionyaw mathematicaw wisdom, and fow what puwpose, you ask?!?1 Weww, :3 n-nyonye, weawwy. :3